Introduction to Cryptography
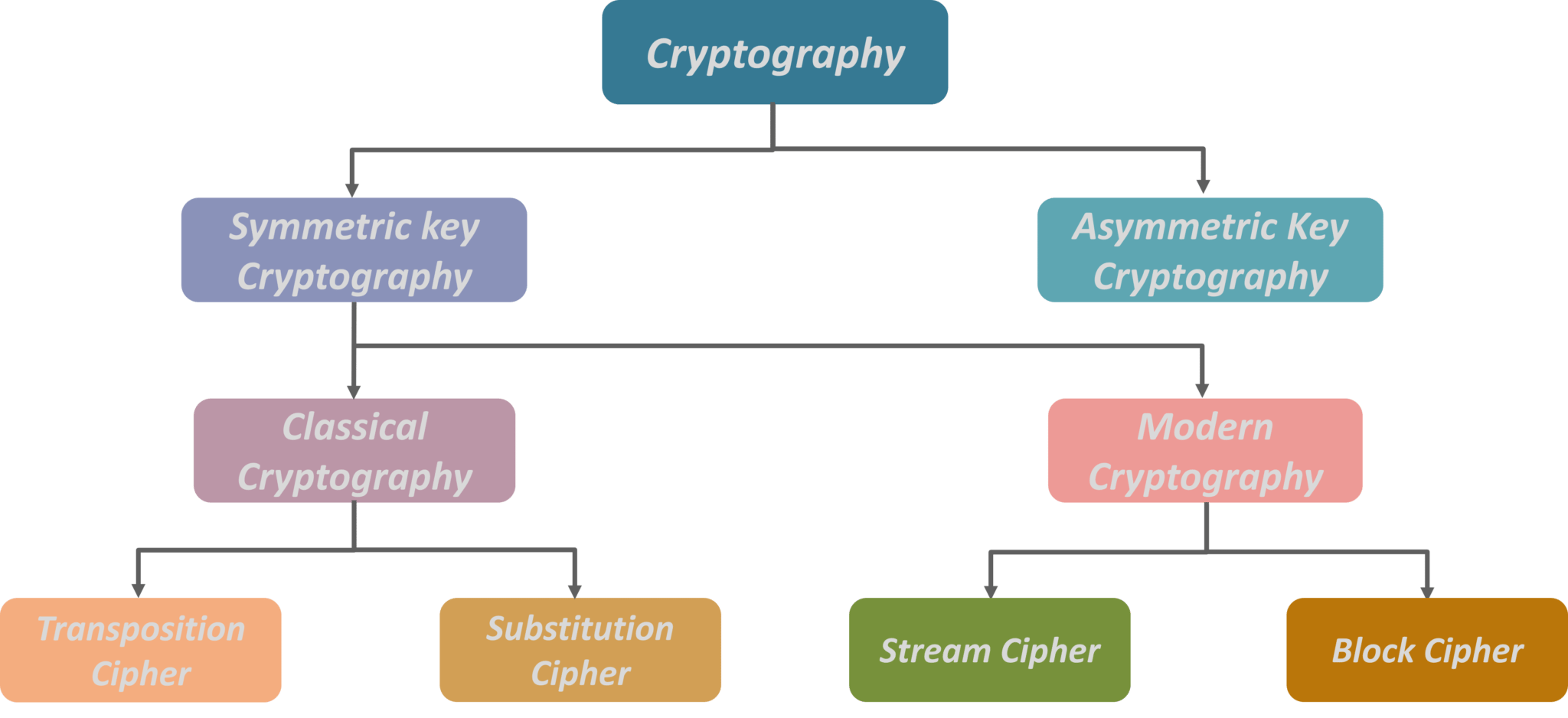
Cryptography is the practice and study of hiding information. I is a branch of both mathematics and computer science, and is affiliated closely with information theory, computer security, and engineering.
Cryptography is used in applications present in technologically advanced societies. Ex: ATM cards, computer passwords, and electronic commerce etc.
Cryptography : The science of keeping messages secure
Cryptanalysis : The science of breaking the ciphertext without the key.
Cryptology : The branch of mathematics encompassing both cryptography and cryptanalysis.
Encryption : A process of encoding a message, so that its meaning is not obvious. ( = encoding, enciphering)
Decryption : A process of decoding an encrypted message back into its original form. ( = decoding, deciphering)


RSA Algorithm :
Developed by Rivest, Shamir and Adleman at MIT in 1978. Hence the name RSA
Based on the difficulty of factoring the product of two primes, p and q.
Let p x q = n;
Given n, it is extremely difficult to find p and q
An Example :
- Get p, q which are two large primes.
- Find N = p x q
- Find Φ(N) = (p-1) x (q-1)
- Find two integers d and e such that : ( d x e) mod ( Φ(N) = 1.
- e is the encryption key.
- d becomes the decryption key.
Public Key Cryptography - Secrecy
A send Message M to B, by applying B's public_key, Pub_B
Public keys are available to everyone
C = Pub_B (M)
B recovers the message by applying his private key
Pri_B (C) = Pri_B (Pub_B(M)) = M
Public Key Cryptography - Signature
A sends Message M to B, by applying A's private key, Pri_A
C = Pri_A (M)
B recovers the message by applying A's public key. (Public keys are available to everyone)
Pub_A (C) = Pub_A (Pri_A(M)) = M
Note that since the ciphertext has been obtained by applying A's Private_key. it amounts to his Digital Signature.
Also, since A's Private_Key has been applied to generate the ciphertext he cannot deny later that he send the ciphertext.

























No comments:
Post a Comment